Fundamentos

     O delineamento casualizado em blocos (dbc) leva em consideração os três princípios básicos da experimentação: repetição, casualização e controle local.
  Para realizar o dcb deve-se repartir a área experimental heterogênea e sub áreas homogêneas.
     Se cada bloco receber todos os tratamentos chama-se de blocos completos, caso algum bloco não receba todos os tratamentos chama-se de blocos imcompletos.

Exemplo: granja de suínos

     Com o objetivo de avaliar o efeito de quatro rações, A, B, C e D, sobre o ganho de peso de animais um pesquisador dispunha do 12 animais com pesos diferentes.
Experimentação animal
Experimentação animal
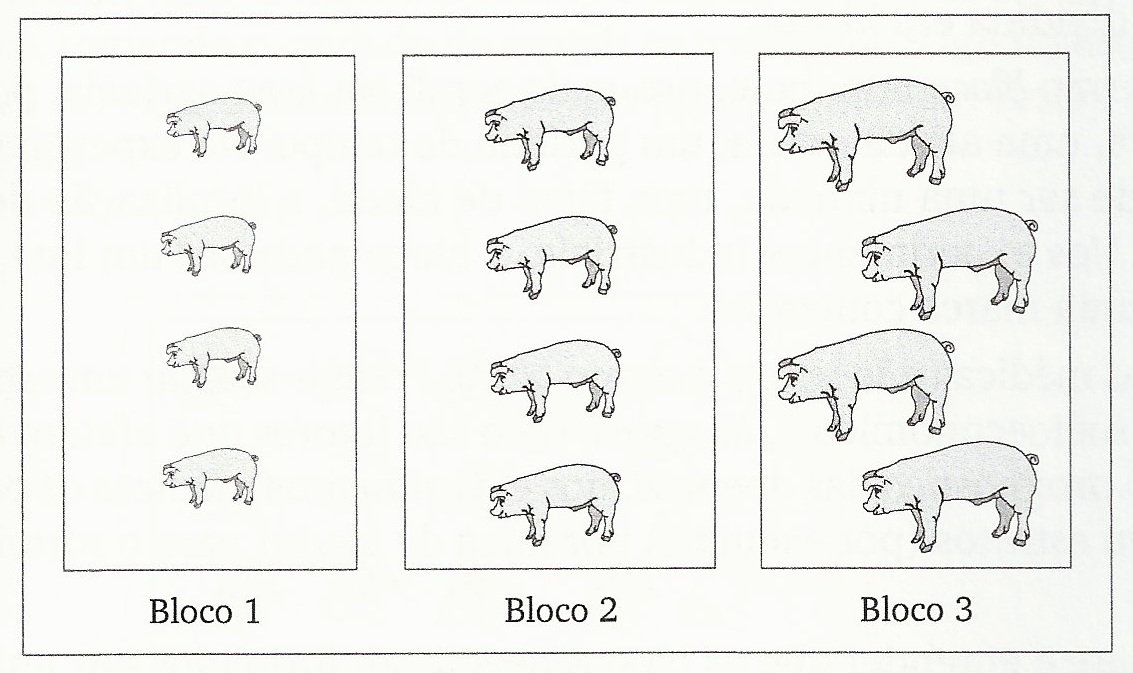
Experimentação animal blocos
Experimentação animal blocos
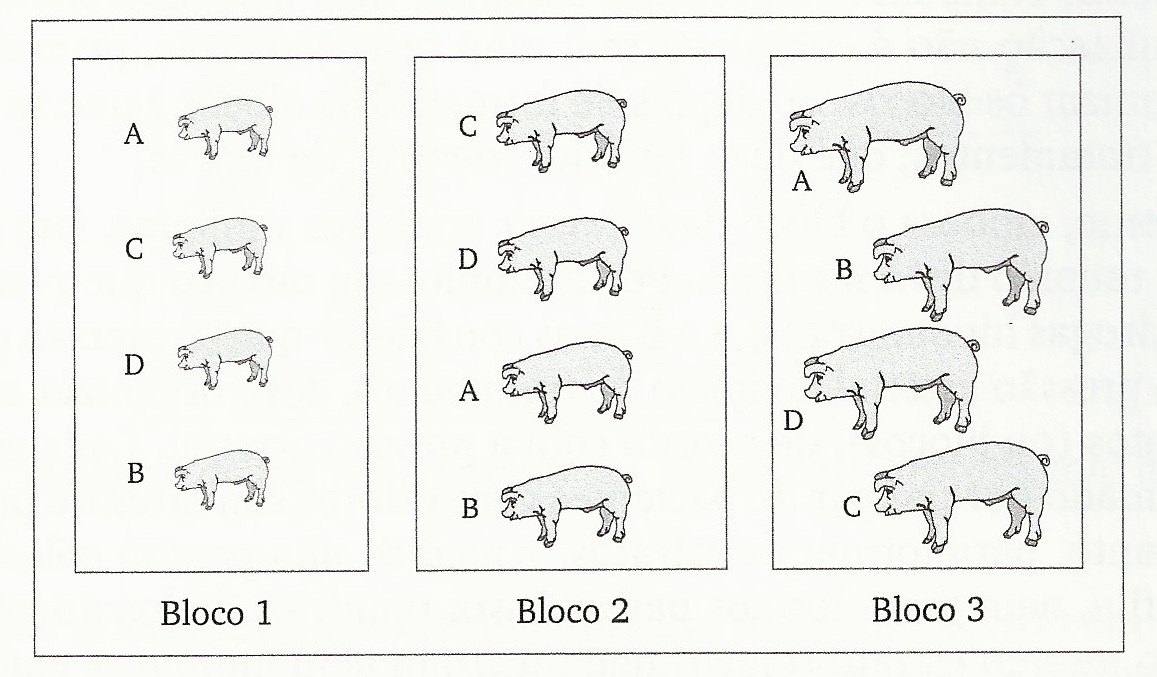
Experimentação animal blocos tratamentos
Experimentação animal blocos tratamentos

Exemplo: Área experimental

Nupea
Nupea

Croqui: comparação entre DIC e DBC

#> [1] "T1" "T2" "T3" "T4" "T5" "T6" "T7" "T8" "T9"
#> 
#> Type 'citation("agricolaeplotr")' for citing this R package in publications.
#> 
#> Attaching package: 'agricolaeplotr'
#> The following object is masked from 'package:base':
#> 
#>     summary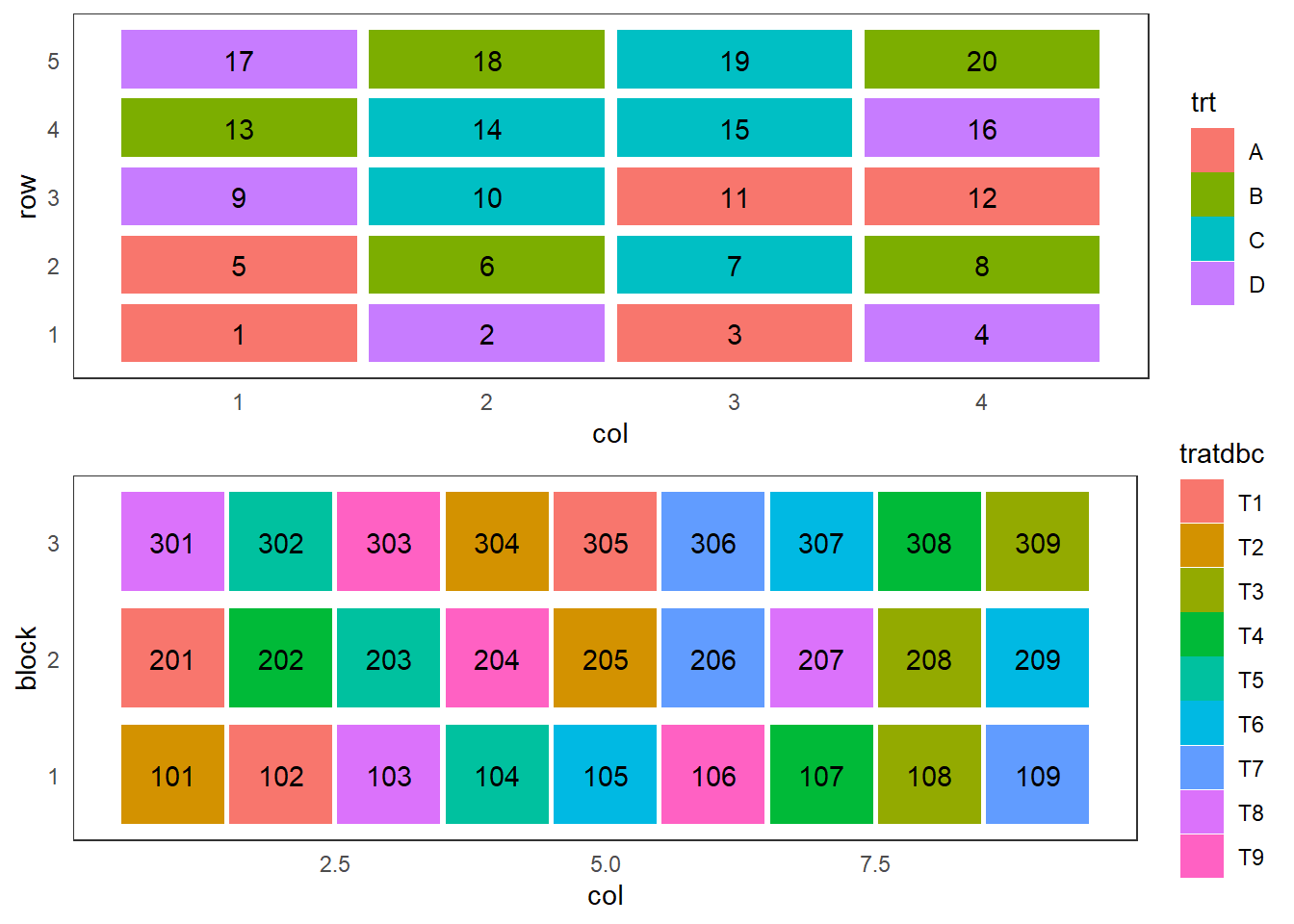

Análise dos dados

Modelo estatístico

\[y_{ij} = \mu + b_j + \tau_i + e_{ij}\text{(1)}\]

em que: - \(y_{ij}\) é a observação referente ao tratamento \(i\) no bloco \(j\);

  • \(\mu\) é a constante comum a todas as observações (média geral);

  • \(b_j\) é o efeito do \(j\)-ésimo bloco, com \(j = 1, 2, \ldots, J\);

  • \(\tau_i\) é o efeito do \(i\)-ésimo tratamento, com \(i = 1, 2, \ldots, I\);

  • \(e_{ij}\) é o erro experimental, tal que \(e_{ij}\sim \mbox{NID} (0; \sigma^2)\).

Estimadores

     As soluções de mínimos quadrados para os parâmetros \(\mu\), \(b_j\) e \(\tau_i\), com \(j=1, \ldots, J\) e \(i = 1, \ldots, I\), assumindo-se as restrições usuais,

\(\sum_{i}\hat{\tau}_i = 0\) e \(\sum_{j}\hat{b}_j = 0\), são:

\[\hat{\mu} = \bar{Y},\] \[\hat{b_j} = \bar{Y}_j - \bar{Y}\] \[\hat{\tau}_i = \bar{Y}_i - \bar{Y}\]

Análise da variância

Hipóteses:

\(H_0:\mu_1 = \mu_2 = \ldots = \mu_I\)

\(H_1:\) pelo menos duas médias de tratamentos diferem entre si

Tabela 1. ANOVA

Fontes de Variação G.L. S.Q. Q.M. F
Blocos \(J - 1\) SQ Blocos
Tratamentos \(I - 1\) SQ Trat QM Trat Fcal
Resíduo \((I-1)(J-1)\) SQ Res QM Res
Total \(IJ - 1\) SQ Total
     Rejeita-se \(H_0\) se \(F_{cal} \geq F_{tab_{(\alpha, I-1, (I-1)(J-1))}}\), em que \(\alpha\) é o nível de significância, \(I-1\) é o número de graus de liberdade do numerador e \((I-1)(J-1)\) é o número de graus de liberdade do denominador.

Exemplo

Os dados apresentados a seguir foram coletados de um experimento instalado no delineamento casualizado em blocos, cujo objetivo é comparar nove porta-enxertos para laranjeira Valência. Cada parcela era constituída por duas plantas e as produções de laranja (número médio de frutos por planta) tomadas dois anos após a instalação do experimento são:

Tabela 2. Numero médio de frutos por porta enxerto

Enxertos I II III Totais Médias
Tangerina sunki 145 155 166 466 155,33
Limão rugoso nacional 200 190 190 580 193,33
Limão rugoso da Flórida 183 186 208 577 192,33
Tangerina Cleópatra 190 175 186 551 183,16
Citranger-troyer 180 160 156 496 165,33
Trifoliata 130 160 130 420 140,00
Tangerina cravo 206 165 170 541 180,33
Laranja caipira 250 271 230 751 250,33
Limão cravo 164 190 193 547 182,33
Totais 1648 1652 1629 4929

Soma de quadrado do Total

\[\text{SQ Total} = \sum_{ij} y_{ij}^2 - \frac{G^2}{IJ} = 145^2 + 155^2 + \ldots + 193^2 - \frac{4929^2}{27} = 27042,67 \]

Soma de quadrado de Blocos

\[\text{SQ Blocos} = \frac{1}{I} \sum_{j} B_{j}^2 - \frac{G^2}{IJ} = \frac{1}{9}\Big(1648^2 + 1652^2 + 1629^2 \Big) - \frac{4929^2}{27} = 33,55 \]

Soma de quadrado de Tratamento

\[\text{SQ Tratamentos} = \frac{1}{J}\sum_{i} T_{i}^2 - \frac{G^2}{IJ} = \frac{1}{3}\Big(466^2 + 580^2 + \ldots + 547^2 \Big) - \frac{4929^2}{27} = 22981,33\]

Soma de quadrado do Resíduo

\[\text{SQ Resíduo} = \text{SQ Total} - \text{SQ Blocos} - \text{SQ Tratamentos} = 27042,67 - 33,55 - 22981,33\\ = 4027,79\]

Tabela 3. Quadro da ANOVA

Fontes de Variação G.L. S.Q. Q.M. F
Blocos 2 33,55 16,78
Tratamentos 8 22.981,33 2.872,67 11,41
Resíduo 16 4.027,79 251,74
Total 26 27.042,67

Tabela F

tabela F
tabela F

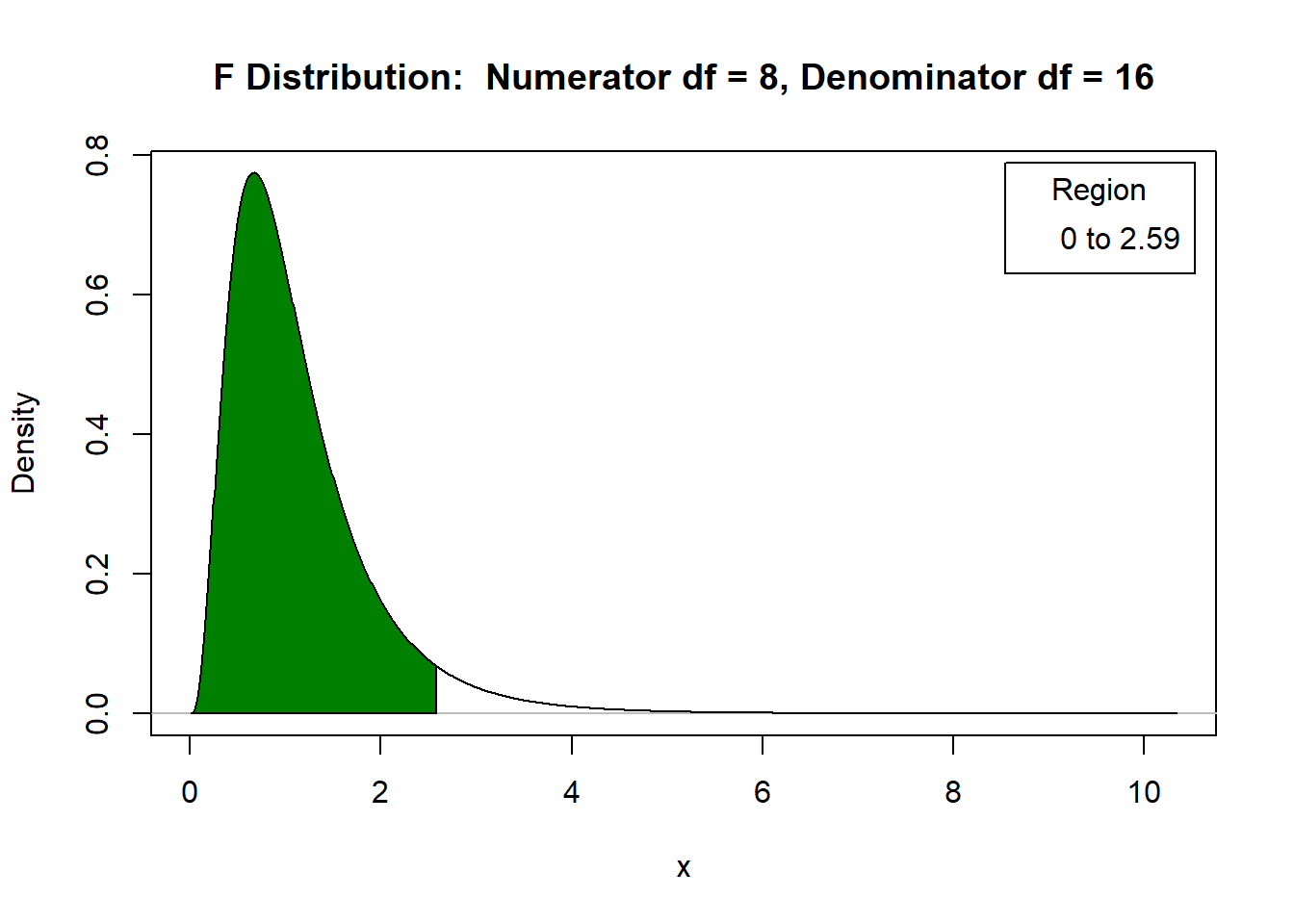
\(F_{(\alpha = 0,05, 8, 16)} = 2,59.\)

Atividades

  1. Com o objetivo de comparar seis diferentes progênies de Eucaliptus grandis com sete anos (médias de 25 plantas por parcela) com relação a altura, em m, um pesquisador instalou um experimento em blocos com quatro repetições. Os dados são apresentados a seguir.
dadose1 <- data.frame(Bloco = as.factor(rep(1:4, each = 6)),
                      Progenie = as.factor(rep(c("Pretoria", 637, 2093,2094,                                                    9559, 9575), times = 4)),
                      
altura = c(20.3,21.7,22.0,20.8,21.5,19.6,
           19.6,19.3,24.9,23.0,22.3,17.7,
           23.5,16.7,24.4,21.3,22.1,18.7,
           19.1,18.5,20.8,24.9,21.9,22.0)
)

Pede-se:

  1. Faça a análise descrita dos dados apresentando comentários
  2. Testar a hipótese de igualdade das médias das progênies ao nível de 5% de significância. Apresentar as hipóteses e conclusões.
  3. Se necessário, comparar as médias das progênies pelo teste de Tukey ao nível de 5% de significância. Apresentar as hipóteses e conclusões
  1. A seguir é apresentado (parcialmente) o quadro da análise da variância dos dados de um estudo realizado em Jaboticabal - SP por Ruiz (1977) que comparou métodos de semeadura no mamoeiro. O experimento foi instalado em delineamento de blocos casualizados, com 4 repetições, avaliando 3 métodos de semeadura. Foram avaliadas duas unidades experimentais por método em cada bloco.
Causa de Variação G.L. S.Q. Q.M. Fcal Ftab
Blocos 7,216 3,16
Tratamentos 8429,1 34,453 3,55
Resíduo 18
Total
\(\hat{\mu}_{A}\) \(\hat{\mu}_{B}\) \(\hat{\mu}_{C}\)
101.05 61.66 60.94

  1. Complete o quadro da ANOVA e conclua.

  2. Faça um teste de médias

Faça o upload da resolução e tire suas aqui