Parcelas subdivididas

Fundamentos

     Considere o seguinte experimento instalado de acordo com o delineamento casualizado em blocos, sendo os fatores de tratamento variedades de soja, com 4 níveis e formas de adubação, com 3 níveis.

\[\mbox{2 fatores} \left\{\begin{array}{l} \mbox{Variedades:} V_1, V_2, V_3, V_4\\ \mbox{Formas}: F_1, F_2, F_3\\ \end{array} \right.\]

\[\Downarrow\] \[\mbox{12 combinações} ⬄ \mbox{12 tratamentos}\]

\[V_1F_1 \; V_1F_2 \; V_1F_3\\ V_2F_1 \; V_2F_2 \; V_2F_3\\ V_3F_1 \; V_3F_2 \; V_3F_3\\ V_4F_1 \; V_4F_2 \; V_4F_3\]

Ensaio Fatorial

1

\[y_{jik} = \mu + b_j + \alpha_{i} + \gamma_k + (\alpha\gamma)_{ik} + e_{jik}.\]

Ensaio em Parcelas Subdivididas

Sorteio dos níveis de Formas casualizados às Parcelas

aula

Possível croqui para um bloco: ensaio em parcelas subdivididas

Sorteio dos níveis de Variedades casualizados às Subparcelas

aula

Possível croqui para um bloco: ensaio em parcelas subdivididas

Ensaio em Faixas

aula

Possível croqui para um bloco: ensaio em faixas

Exemplo de um Delineamento Casualizado em Blocos com parcelas subdivididas

     O vírus da batata Y (PVY) é uma séria ameaça à produção de batata devido aos efeitos no rendimento e na qualidade dos tubérculos, em particular, devido à indução de doença de mancha anelar necrótica do tubérculo da batateira (PTNRD), tipicamente associada com cepas recombinantes de PVY.

      Essas cepas recombinantes têm se espalhado nos Estados Unidos nos últimos anos, embora as razões para essa disseminação contínua permaneçam obscuras. Para documentar e avaliar esta propagação entre 2011 e 2015, a composição da cepa de isolados de PVY que circulam na área de produção de batata da Columbia Basin foi determinada a partir de centenas de lotes de sementes de vários cultivares. Para abordar ainda mais a mudança na abundância de cepas, experimentos em casa de vegetação foram conduzidos (Funke et al, 2017, Plant Disease 101:20-28,

artigo.

A, Croqui do experimento em casa de vegetação, mostrando as dimensões das parcelas e o delineamento casualizado em blocos.

As letras indicam plantas de batata individuais:

• B = Russet Burbank,
• U = Umatilla Russet,
• R = Ranger Russet e
• A = Alturas.

     A cor de sombreamento designa a cepa do virus de batata Y (PVY) usada para inoculação: verde significa PVY O (isolado Tb60), azul significa PVY N-Wi (isolado N1), rosa significa PVY NTN (isolado HR1) e sem sombreamento significa não inoculado.

B, Imagem da casa de vegetação antes da inoculação com isolados de PVY.

aula

     Ensaios em parcelas subdivididas podem ser instalados em qualquer delineamento experimental (DIC, DBC,DQL); assim como os fatoriais, também envolvem as combinações dos níveis dos fatores de tratamento.

aula

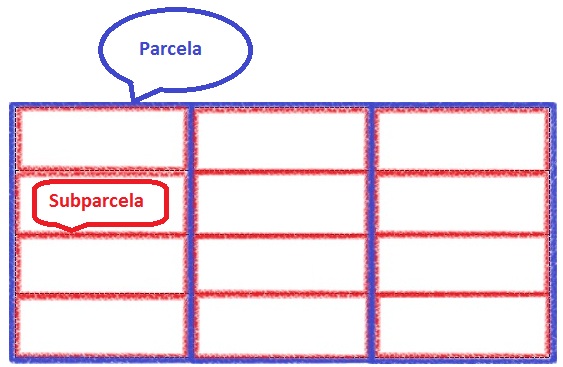
• Fator primário: casualizado às parcelas;
• Fator secundário: casualizado às subparcelas.

Observações

• Os níveis do fator secundário são mais sorteados \(arrow\) maior precisão;
• Deve-se, preferencialmente, alocar os níveis do fator de maior interesse na subparcela;
• A ANOVA terá dois resíduos, um para parcelas e outro para subparcelas;
• Teremos dois coeficientes de variação, um ao nível de parcela, e outro ao nível de subparcela.

Análise dos dados

Modelo estatístico

     Supondo um experimento instalado de acordo com o delineamento casualizado em blocos, sendo \(r\) o número de blocos, e esquema de tratamento em parcelas subdivididas, com o fator primário \(A\), com \(a\) níveis e o fator secundário \(B\), com \(b\) níveis.

\[y_{jik} = \mu + b_j + \alpha_i + e_{ji} + \gamma_k + (\alpha\gamma)_{ik} + \epsilon_{jik}, \; j=1,\ldots, r, \; i=1,\ldots, a, \; k=1,\ldots, b,\]

em que \(y_{jik}\), é o valor observado no \(j\)-ésimo bloco, \(i\)-ésimo nível do fator \(A\) e \(k\)-ésimo nível do fator \(B\),

• \(\mu\) é uma constante,
• \(b_j\) é o efeito do \(j\)-ésimo bloco,
• \(\alpha_i\) é o efeito do \(i\)-ésimo nível do fator \(A\),
• \(e_{ji}\) é o erro experimental associado às parcelas, tais que \(e_{ji}\sim N(0, \sigma^2_P)\),
• \(\gamma_k\) é o efeito do \(k\)-ésimo nível do fator \(B\),
• \((\alpha\gamma)_{ik}\) é o efeito da interação entre o \(i\)-ésimo nível do fator \(A\) e o \(k\)-ésimo nível do fator \(B\),\ \(\epsilon_{jik}\) é o erro experimental associado às subparcelas, tais que \(\epsilon_{jik} \sim N(0, \sigma^2)\).

Esquema da ANOVA

      Considere um experimento instalado de acordo com o delineamento casualizado em blocos com três repetições, em um esquema de tratamentos em parcelas subdivididas, sendo o fator primário formas de adubação, com três níveis, e o fator secundário variedades de soja, com 4 níveis.

Se considerarmos somente parcelas

aula

F.V.	gl
Blocos	\(3-1 = 2\)
Fator A	\(3-1 = 2\)
Resíduo (a)	\((3-1)(3-1) = 4\)
(Parcelas)	\((3\times3-1 = 8)\)

Entretanto, os níveis de Variedade foram casualizados às subparcelas

aula

F.V.	gl
Blocos	\(3-1 = 2\)
Forma	\(3-1 = 2\)
Resíduo (a)	\((3-1)(3-1) = 4\)
(Parcelas)	\((3\times3-1) = 8\)
Variedade	\(4-1 = 3\)
Forma#Variedade	\((3-1)(4-1) = 6\)
Resíduo (b)	\(3(4-1)(3-1) = 18\)
Total (Subparcelas)	\(3\times3\times4 - 1 = 35\)

     Supondo um experimento instalado de acordo com o delineamento casualizado em blocos, sendo \(r\) o número de blocos, e esquema de tratamento em parcelas subdivididas, com o fator primário \(A\), com \(a\) níveis e o fator secundário \(B\), com \(b\) níveis.

Fator \(A\)	Fator \(B\)	Bloco1	Bloco2	\(\cdots\)	\(r\)	Totais
\(A_1\)	\(B_1\)	\(y_{111}\)	\(y_{211}\)	\(\cdots\)	\(y_{r11}\)	\(T_1 = y_{.11}\)
-	\(B_2\)	\(y_{112}\)	\(y_{212}\)	\(\cdots\)	\(y_{r12}\)	\(T_2 = y_{.12}\)
-	\(\cdots\)	\(\cdots\)	\(\cdots\)	\(\cdots\)	\(\cdots\)	\(\cdots\)
\(A_2\)	\(B_1\)	\(y_{121}\)	\(y_{221}\)	\(\cdots\)	\(y_{r21}\)	\(T_{b+1} = y_{.21}\)
-	\(B_2\)	\(y_{122}\)	\(y_{222}\)	\(\cdots\)	\(y_{r22}\)	\(T_{b+2} = y_{.22}\)
-	\(\cdots\)	\(\cdots\)	\(\cdots\)	\(\cdots\)	\(\cdots\)	\(\cdots\)
-	\(B_b\)	\(y_{12b}\)	\(y_{22b}\)	\(\cdots\)	\(y_{r2b}\)	\(T_{2b} = y_{.2b}\)
\(A_a\)	\(B_1\)	\(y_{1a1}\)	\(y_{2a1}\)	\(\cdots\)	\(y_{ra1}\)	\(T_{b(a-1)+1} = y_{.a1}\)
-	\(B_2\)	\(y_{1a2}\)	\(y_{2a2}\)	\(\cdots\)	\(y_{ra2}\)	\(T_{b(a-1)+2} = y_{.a2}\)
-	\(\cdots\)	\(\cdots\)	\(\cdots\)	\(\cdots\)	\(\cdots\)	\(\cdots\)
Totais	-	\(R_1 = y_{1..}\)	\(R_2 = y_{2..}\)	\(\cdots\)	\(R_r = y_{r..}\)	\(G = y_{...}\)

Nota: No exemplo, \(r=3\), \(a = 3\) e \(b = 4\).

Soma de quadrados do Total

\[\displaystyle{SQ_{\text{Total}} = \sum_j\sum_i\sum_k y_{jik}^2 - \frac{(\sum_j\sum_i\sum_k y_{jik})^2}{rab}}.\]

Soma de quadrados da Parcela

\[\displaystyle{SQ_{\text{Parcela}} = \frac{1}{b}\sum_j\sum_i y_{ji.}^2 - \frac{(\sum_j\sum_i\sum_k y_{jik})^2}{rab}}.\]

Soma de quadrados do Fator \(A\)

\[\displaystyle{SQ_{\text{Fator A}} = \frac{1}{rb}\sum_i T_{A_i}^2 - \frac{(\sum_j\sum_i\sum_k y_{jik})^2}{rab}}.\]

Quadro auxiliar com os totais para as combinações dos níveis de Blocos e Fator A.

Soma de quadrados do Resíduo (a)

\[\displaystyle{SQ_{\text{Res (a)}} = SQ_\text{Parcela} - SQ_\text{Blocos} - SQ_\text{Fator A}}.\]

Soma de quadrados do Fator B

\[\displaystyle{SQ_{\text{Fator B}} = \frac{1}{ra}\sum_k T_{B_k}^2 - \frac{(\sum_j\sum_i\sum_k y_{jik})^2}{rab}}.\]

Soma de quadrados da combinação \(A,B\) (Tratamentos)

\[\displaystyle{SQ_{A,B} = \frac{1}{r}\sum_i\sum_k y_{.ij}^2 - \frac{(\sum_j\sum_i\sum_k y_{jik})^2}{rab}}.\]

Soma de quadrados da Interação \(A\#B\)

\[\displaystyle{SQ_{A\#B} = SQ_{A,B} - SQ_\text{Fator A} - SQ_\text{FAtor B}}.\]

Soma de quadrados do Resíduo (b)

\[\displaystyle{SQ_\text{Res (b)} = SQ_\text{Total} - SQ_\text{Parcela} - SQ_\text{Fator B} - SQ_{A\#B}}.\]

Esquema da ANOVA - Generalizando

F.V.	gl	SQ	QM	F
Blocos	\(r-1\)	SQ Blocos	-	-
Fator A	\(a-1\)	SQ A	QM A	\(\frac{\mbox{QM A}}{\mbox{QM Res(a)}}\)
Resíduo (a)	\((r-1)(a-1)\)	SQ Res(a)	QM Res(a)	-
(Parcelas)	\((ar-1)\)	(SQ Parcelas)	-	-
Fator B	\(b-1\)	SQ B	QM B	\(\frac{\mbox{QM B}}{\mbox{{QM Res(b)}}}\)
Int A#B	\((a-1)(b-1)\)	SQ Int A#B	QM Int A#B	\(\frac{\mbox{QM Int A\#B}}{{\mbox{QM Res(b)}}}\)
Resíduo (b)	\(a(b-1)(r-1)\)	SQ Res(b)	QM Res(b)	-
Total	\(abr-1\)	SQ Total	-	-

Interação não Significativa

• Avaliar efeito principal do Fator A;
• Avaliar efeito principal do Fator B;

Caso algum efeito seja significativo, realizar teste de comparações múltiplas e/ou estudo de regressão.

Interação Significativa

• Avaliar efeito do Fator B dentro de cada nível do Fator A \(arrow\) QMRes (b);

• Avaliar efeito do Fator A dentro de cada nível do Fator B \(arrow\) QMRes Composto;

Exemplo

Banzatto e Kronka (1992), apresentaram o ensaio citado por Steel e Torrie (1980), no qual são comparadas 4 variedades de aveia e 4 tratamentos de sementes quanto aos efeitos sobre a produção. As variedades foram casualizadas às parcelas de cada um dos quatro blocos do ensaio. Os tratamentos de sementes foram casualizados às quatro subparcelas de cada parcela.

Variedades de aveia:

\(A_1\) - Vicland 1 infectada com o fungo {} \(A_2\) - Vicland 2 não infectada \(A_3\) - Clinton resistente a {} \(A_4\) - Branch resistente a {}

Tratamentos de sementes:

\(B_1\) - Testemunha \(B_2\) - Ceresan M \(B_3\) - Panogem \(B_4\) - Agros

Variedades (A)	Tratamento de sementes (B)	Bl1	Bl2	Bl3	Bl4	Totais	Médias
\(A_1\)	\(B_1\)	42,9	41,6	28,9	30,8	144,2	36,050
-	\(B_2\)	53,8	58,5	43,9	46,3	202,5	50,625
-	\(B_3\)	49,5	53,8	40,7	39,4	183,4	45,850
-	\(B_4\)	44,4	41,8	28,3	34,7	149,2	37,300
\(A_2\)	\(B_1\)	53,3	69,6	45,4	35,1	203,4	50,850
-	\(B_2\)	57,6	69,6	42,4	51,9	221,5	55,375
-	\(B_3\)	59,8	65,8	41,4	45,4	212,4	53,100
-	\(B_4\)	64,1	57,4	44,1	51,6	217,2	54,300
\(A_3\)	\(B_1\)	62,3	58,5	44,6	50,3	215,7	53,925
-	\(B_2\)	63,4	50,4	45,0	46,7	205,5	51,375
-	\(B_3\)	64,5	46,1	62,6	50,3	223,5	55,875
-	\(B_4\)	63,6	56,1	52,7	51,8	224,2	56,050
\(A_4\)	\(B_1\)	75,4	65,6	54,0	52,7	247,7	61,925
-	\(B_2\)	70,3	67,3	57,6	58,5	253,7	63,425
-	\(B_3\)	68,8	65,3	45,6	51,0	230,7	57,675
-	\(B_4\)	71,6	69,4	56,6	47,4	245,0	61,250
Totais	-	965,3	936,8	733,8	743,9	3379,8	52,809

Efeitos principais

aula

Variedade	B1	B2	B3	B4
A1	36,050	50,625	45,850	37,30
A2	50,850	55,375	53,100	54,30
A3	53,925	51,375	55,875	56,05
A4	61,925	63,425	57,675	61,25
médias	50,688	55,200	53,125	52,225

aula

Exemplo: Efeitos simples e de interação

aula

\[SQTotal = \sum_{jik}y_{jik}^2 - \frac{y_{\cdot\cdot\cdot}^2}{rab} \\ \nonumber = {42,9}^2 + {53,8}^2 + \ldots + {47,4}^2 - \frac{{3379,8}^2}{64} = 7797,39 \]

Fontes de Variação	gl	SQ	QM
Blocos	3
A	\(3\)	{2848,02}	{949,34}
Resíduo (a)	\(9\)	{618,30}	{68,70}
(Parcelas)	\((15)\)	{3466,32}
B	\(3\)	{170,53}	{56,84}
A#B	\(9\)	{586,47}	{65,16}
Resíduo (b)	\(36\)	{731,20}	{20,31}
Total	63	7797,39

Tabela auxiliar: Envolve a repetição (ou blocos) e o tratamento de parcela.

Variedades (A)	I	II	III	IV
A1	190,6(4)	195,7(4)	141,8(4)	151,2(4)
A2	234,8(4)	262,4(4)	173,3(4)	184,0(4)
A3	253,8(4)	211,1(4)	204,9(4)	199,1(4)
A4	286,1(4)	267,6(4)	213,8(4)	209,6(4)
Totais	965,3(16)	936,8(16)	733,8(16)	743,9(16)

\[SQBlocos = \frac{1}{ab}\sum_{j}y_{j\cdot\cdot}^2 - \frac{y_{\cdot\cdot\cdot}^2}{rab} \\ \nonumber = \frac{1}{16}\Big({965,3}^2 + {936,8}^2 + {733,8}^2 + {743,9}^2 \Big) - \frac{{3379,8}^2}{64} \\ = 2842,87\]

\[SQParcelas = \frac{1}{b}\sum_{ji}y_{ji\cdot}^2 - \frac{y_{\cdot\cdot\cdot}^2}{rab}\\ \nonumber = \frac{1}{4}\Big({190,6}^2 + {234,8}^2 + \ldots + {209,6}^2\Big) - \frac{{3379,8}^2}{64} \\ \nonumber = 6309,19 \]

\[SQA = \frac{1}{rb}\sum_{i}y_{\cdot i\cdot}^2 - \frac{y_{\cdot\cdot\cdot}^2}{rab} \\ \nonumber = \frac{1}{16}\Big({679,3}^2+{854,5}^2+{868,9}^2+{977,1}^2\Big) - \frac{{3379,8}^2}{64} \\ \nonumber = 2848,02 \]

Fontes de Variação	gl	SQ	QM	F
Blocos	3	2842,87
A	\(3\)	2848,02	{949,34}	{13,82
Resíduo (a)	\(9\)	618,30	{68,70}
(Parcelas)	\((15)\)	(6309,19)
B	\(3\)	{170,53}	{56,84}	{2,80}
A#B	\(9\)	{586,47}	{65,16}	{3,21}
Resíduo (b)	\(36\)	{731,20}	{20,31}
Total	63	7797,39

\[SQRes(a) = SQParcelas - SQBlocos - SQA = 6309,19-2842,87-2848,02 = 618,30\]

Tabela auxiliar: Envolve o tratamento de parcela e de subparcela.

Variedades (A)	B1	B2	B3	B4
A1	144,2(4)	202,5(4)	183,4(4)	149,2(4)
A2	203,4(4)	221,5(4)	212,4(4)	217,2(4)
A3	215,7(4)	205,5(4)	223,5(4)	224,2(4)
A4	247,7(4)	253,7(4)	230,7(4)	245,0(4)
Totais	811,0(16)	883,2(16)	850,0(16)	835,6(16)

\[SQB = \frac{1}{ra}\sum_ky_{\cdot \cdot k^2} - \frac{y_{\cdot\cdot\cdot^2}}{rab} \\ = \frac{1}{16}\Big({811,0}^2 + {883,2}^2+{850,0}^2+{835,6}^2\Big) - \frac{{3379,8}^2}{64} \\ \nonumber = 170,53 \]\

\[SQA,B = \frac{1}{r}\sum_{ik} y_{\cdot ik^2} - \frac{y_{\cdot\cdot\cdot^2}}{rab} \\ \nonumber = \frac{1}{4}\Big({144,2}^2 + {203,4}^2+ \ldots +{245,0}^2\Big) - \frac{{3379,8}^2}{64} \\ \nonumber = 3605,02 \\\]

Fontes de Variação	gl	SQ	QM
Blocos	3	2842,87
A	\(3\)	2848,02	{949,34}
Resíduo (a)	\(9\)	618,30	{68,70}
(Parcelas)	\((15)\)	(6309,19)
B	\(3\)	170,53	{56,84}
A#B	\(9\)	586,47	{65,16}
Resíduo (b)	\(36\)	731,20	{20,31}\
Total	63	7797,39

\[ SQA\#B = SQA,B - SQA - SQB\\ \nonumber = 3605,02 - 2848,02 - 170,53 = 586,47 \\ \nonumber SQRes(b) = SQTotal - SQParcelas - SQB - SQA\#B \\ \nonumber = 7797,39 - 6309,19 - 170,53 - 586,47 = 731,20\] \

Fontes de Variação	gl	SQ	QM	F	F\(_\text{tab}(\alpha = 0,05)\)\
Blocos	3	2842,87		\
A	\(3\)	2848,02	949,34	13,82	3,86\
Resíduo (a)	\(9\)	618,30	68,70	\
(Parcelas)	\((15)\)	(6309,19)		\
B	\(3\)	170,53	56,84	2,80	2,87\
{A#B}	{\(9\)}	{586,47}	{65,16}	{3,21}	{2,15}\
Resíduo (b)	\(36\)	731,20	20,31\
Total	63	7797,39		\

Hipóteses:\ { \(H_0:\) Não há efeito da interação \ \(H_1:\) Há efeito da interação.}

Como \(F = 3,21 > 2,15 = F_\text{tab}(\alpha = 0,05)\), com nível de 5% de significância, rejeita-se \(H_0\). Desse modo, há evidências para afirmarmos que há efeito da interação entre os fatores. Sendo assim, serão avaliados os efeitos simples.

Exemplo: Efeito de Tratamento de Sementes dentro de cada Variedade}

\(H_0: \mu_{A1{B1}} = \mu_{A1{B2}} = \mu_{A1{B3}} = \mu_{A1{B4}}\) \(H_1: \text{Pelo menos duas médias diferente entre si}\)

\(SQ B d.A1= \frac{1}{4}\Big({144,2}^2+{202,5}^2+{183,4}^2+{149,2}^2\Big)- \frac{{679,3}^2}{16}=583,49\)\

Exemplo: Efeito de Tratamento de Sementes dentro de cada Variedade}

\(H_0: \mu_{A2{B1}} = \mu_{A2{B2}} = \mu_{A2{B3}} = \mu_{A2{B4}}\) \(H_1: \text{Pelo menos duas médias diferente entre si}\)

\(SQ B d.A2=\frac{1}{4}\Big({ 203,4}^2+{221,5}^2+{212,4}^2+{217,2}^2\Big)- \frac{{854,5}^2}{16}=45,21\)\

Exemplo: Efeito de Tratamento de Sementes dentro de cada Variedade

\(H_0: \mu_{A3{B1}} = \mu_{A3{B2}} = \mu_{A3{B3}} = \mu_{A3{B4}}\) \(H_1: \text{Pelo menos duas médias diferente entre si}\)

\(SQ B d.A3=\frac{1}{4}\Big({215,7}^2+{205,5}^2+{223,5}^2+{224,2}^2\Big)- \frac{{868,9}^2}{16}=56,96\)\

Exemplo: Efeito de Tratamento de Sementes dentro de cada Variedade}

\(H_0: \mu_{A4{B1}} = \mu_{A4{B2}} = \mu_{A4{B3}} = \mu_{A4{B4}}\) \(H_1: \text{Pelo menos duas médias diferentes entre si}\)

\(SQ B d.A4=\frac{1}{4}\Big({247,7}^2+{253,7}^2+{230,7}^2+{245,0}^2\Big)- \frac{{977,1}^2}{16}=71,34\)\

Exemplo: Efeito de Tratamento de Sementes dentro de cada Variedade}

Fontes de Variação | gl | SQ | QM | Fcal | F_(\(\alpha = 0,05\)) -|-|-|-|-|\ B d. A1 | 3 | 583,49 | 194,50 | 9,58 | 2,87\ B d. A2 | 3 | 45,21 | 15,07 | 0,74 | 2,87\ B d. A3 | 3 | 56,96 | 18,99 | 0,94 | 2,87\ B d. A4 | 3 | 71,34 | 23,78 | 1,17 | 2,87\ Resíduo (b) | 36 | 731,20 | 20,31 | | \

Ao nível de 5% de significância, há efeito de tratamentos de sementes dentro da variedade A1. Considerando-se as demais variedades, não há efeito significativo de tratamento de sementes.

Exemplo: Efeito de Tratamento de Sementes dentro de cada Variedade

Teste de Tukey para tratamentos de sementes dentro da variedade A1

\[\Delta = q_{(5\%, b, \text{gl Res (b)})}\sqrt{\frac{QMRes(b)}{r}} = 3,81\sqrt{\frac{20,31}{4}} = 8,585\]

\(\hat{\mu}_{A_1B_3} = 45,850\)  \(\hat{\mu}_{A_1B_4} = 37,300\)  \(\hat{\mu}_{A_1B_1} = 36,050\) \

\(\hat{\mu}_{A_1B_2} = 50,625\) | 4,775 | {13,325} | {14,575} \
\(\hat{\mu}_{A_1B_3} = 45,850\) | | 8,550 | {9,800} \ \(\hat{\mu}_{A_1B_4} = 37,300\) | | | 1,250 \

aula

Médias	Classificação
\(\hat{\mu}_{A_1B_2}=50,625\)	a
\(\hat{\mu}_{A_1B_3}=45,850\)	a b
\(\hat{\mu}_{A_1B_4}=37,300\)	b c
\(\hat{\mu}_{A_1B_1}=36,050\)	c

aula

Variedade	B1	B2	B3	B4
A1	36,050 ; C	50,625 ; A	45,850 ;A B	37,30 ; B C
A2	50,850 ; A	55,375 ; A	53,100 ;A	54,30 ; A
A3	53,925 ; A	51,375 ; A	55,875 ; A	56,05 ; A
A4	61,925 ; A	63,425 ;A	57,675 ; A	61,25 ; A
médias	50,688	55,200	53,125	52,225

Teste de Tukey para tratamentos de sementes dentro da variedade A1

\[\Delta = q_{(5\%, b, \text{gl Res (b)})}\sqrt{\frac{QMRes(b)}{r}} = 3,81\sqrt{\frac{20,31}{4}} = 8,585\]

média	Classificação
\(\hat{\mu}_{A_1B_2}=50,625\)	a
\(\hat{\mu}_{A_1B_3}=45,850\)	a b
\(\hat{\mu}_{A_1B_4}=37,300\)	b c
\(\hat{\mu}_{A_1B_1}=36,050\)	c

      De acordo com o teste de Tukey, ao nível de 5% de significância, há evidências para afirmar que a produção média para o tratamento de sementes B2 difere da produção média para os tratamentos de sementes B1 e B4, sendo B2 o que apresentou maior produção. Ainda, há evidências para afirmar que a produção média para o tratamento de sementes B3 difere da produção média para o tratamento de sementes B1 e as demais médias não apresentaram diferença significativa.

\(H_0: \mu_{{A1}B1} = \mu_{{A2}B1} = \mu_{{A3}B1} = \mu_{{A4}B1}\)\ \(H_1: \text{Pelo menos duas médias diferem entre si}\)

\(SQ A d.B1=\frac{1}{4}\Big({144,2}^2+{203,4}^2+{215,7}^2+{247,7}^2\Big)- \frac{{811,0}^2}{16}=1.404,18\)\

\(H_0: \mu_{{A1}B2} = \mu_{{A2}B2} = \mu_{{A3}B2} = \mu_{{A4}B2}\)\ \(H_1: \text{Pelo menos duas médias diferem entre si}\)

\(SQ A d.B2=\frac{1}{4}\Big({202,5}^2+{221,5}^2+{205,5}^2+{253,7}^2\Big)- \frac{{883,2}^2}{16}=412,97\)\

{ {Exemplo: Efeito de Variedades dentro de cada Tratamento de Sementes}

\(H_0: \mu_{{A1}B3} = \mu_{{A2}B3} = \mu_{{A3}B3} = \mu_{{A4}B3}\)\ \(H_1: \text{Pelo menos duas médias diferem entre si}\)

\(SQ A d.B3=\frac{1}{4}\Big({183,4}^2+{212,4}^2+{223,5}^2+{230,7}^2\Big)-\frac{{850,0}^2}{16}=324,77\)\

{Exemplo: Efeito de Variedades dentro de cada Tratamento de Sementes}

\(H_0: \mu_{{A1}B4} = \mu_{{A2}B4} = \mu_{{A3}B4} = \mu_{{A4}B4}\)\ \(H_1: \text{Pelo menos duas médias diferem entre si}\)

\(SQ A d.B4=\frac{1}{4}\Big({149,2}^2+{217,2}^2+{224,2}^2+{245,0}^2\Big)-\frac{{835,6}^2}{16}=1.292,57\)

{ {Exemplo: Efeito de Variedades dentro de cada Tratamento de Sementes}

\[QM*\text{Resíduo Composto} \|=\| \frac{QM \text{Resíduo (a)}+(b-1)QM \text{Resíduo (b)}}{b} \\ \nonumber \|=\| \frac{68,70+(4-1)20,31}{4}=32,41\]

\[\nu \|=\|\frac{[QM \text{Resíduo (a)}+(b-1)QM \text{Resíduo (b)}]^2}{\frac{[QM \text{Resíduo (a)}]^2}{gl \text{Resíduo (a)}}+ \frac{[(b-1)QM \text{Resíduo (b)}]^2}{gl \text{Resíduo (b)}}} \\ \nonumber \|=\| \frac{[68,70+(4-1)20,31]^2}{[68,70]^2/9+[(4-1)20,31]^2/36} \approx26,78\approx27 gl\]

{ {Exemplo: Efeito de Variedades dentro de cada Tratamento de Sementes}

Fontes de Variação	gl	SQ	QM	Fcal	\(F_\text{tab}(\alpha = 0,05)\) \
A d. B1	3	1.404,18	468,06	14,44	2,96 \
A d. B2	3	412,97	137,66	4,25	2,96 \
A d. B3	3	324,77	108,26	3,34	2,96 \
A d. B4	3	1.292,57	430,86	13,29	2,96 \
Resíduo Composto	27		32,41		\

De acordo com o teste F, ao nível de 5% de significância, há efidências para afirmar que há efeito significativa de Variedades dentro de cada um dos tratamentos de sementes.

{Exemplo: Efeito de Variedades dentro de cada Tratamento de Sementes} { Teste de Tukey para comparação de médias de Variedades dentro de cada Tratamento de sementes

\[\Delta=q_{(5\%, a, gl \text{Res Composto})}\sqrt{\frac{\text{QM Resíduo Composto}}{r}}=3,88\sqrt{\frac{32,41}{4}}=11,0\]

Variedades dentro de B1 (Testemunha)}

\(\hat{\mu}_{A_3B_1} = 53,925\) | \(\hat{\mu}_{A_2B_1} = 50,850\) | \(\hat{\mu}_{A_1B_1} = 36,050\) \

\(\hat{\mu}_{A_4B_1} = 61,925\) | 8,000 | {11,075} | {25,875} \
\(\hat{\mu}_{A_3B_1} = 53,925\) | | 3,075 | {17,875} \ \(\hat{\mu}_{A_2B_1} = 50,850\) | | | {14,800} \

aula

média	Classificação
\(\hat{\mu}_{A_4B_1}=61,925\)	a
\(\hat{\mu}_{A_3B_1}=53,925\)	a b
\(\hat{\mu}_{A_2B_1}=50,850\)	b
\(\hat{\mu}_{A_1B_1}=36,050\)	c

B2 { {Exemplo: Efeito de Variedades dentro de cada Tratamento de Sementes} { Teste de Tukey para comparação de médias de Variedades dentro de cada Tratamento de sementes

\[\Delta=q_{(5\%, a, gl \text{Res Composto})}\sqrt{\frac{\text{QM Resíduo Composto}}{r}}=3,88\sqrt{\frac{32,41}{4}}=11,0\]

Variedades dentro de B2 (Ceresan M)}

\(\hat{\mu}_{A_2B_2} = 55,375\) | \(\hat{\mu}_{A_3B_2} = 51,375\) | \(\hat{\mu}_{A_1B_2} = 50,625\) \ \(\hat{\mu}_{A_4B_2} = 63,425\) | 8,050 | {12,050} | {12,800} \
\(\hat{\mu}_{A_2B_2} = 55,375\) | | 4,000 | 4,750 \ \(\hat{\mu}_{A_3B_2} = 51,375\) | | | 0,750 \

aula

média	classificação
\(\hat{\mu}_{A_4B_2}=63,425\)	a
\(\hat{\mu}_{A_2B_2}=55,375\)	a b
\(\hat{\mu}_{A_3B_2}=51,375\)	b
\(\hat{\mu}_{A_1B_2}=50,625\)	b

B3 Exemplo: Efeito de Variedades dentro de cada Tratamento de Sementes} { Teste de Tukey para comparação de médias de Variedades dentro de cada Tratamento de sementes

\[\Delta=q_{(5\%, a, gl \text{Res Composto})}\sqrt{\frac{\text{QM Resíduo Composto}}{r}}=3,88\sqrt{\frac{32,41}{4}}=11,0\]

Variedades dentro de B3 (Panogen)}

\(hat{mu}_{A_3B_3} = 55,875\) | \(hat{mu}_{A_2B_3} = 53,100\) | \(hat{mu}_{A_1B_3} = 45,850\)

\(hat{mu}_{A_4B_3} = 57,675\) | 1,800 | 4,575 | {11,825} \(hat{mu}_{A_3B_3} = 55,875\) | | 2,775 | 10,025 \(\hat{mu}_{A_2B_3} = 53,100\) | | | 7,250

aula

média	classificação
\(\hat{\mu}_{A_4B_3}=57,675\)	a
\(\hat{\mu}_{A_3B_3}=55,875\)	a b
\(\hat{\mu}_{A_2B_3}=53,100\)	ab
\(\hat{\mu}_{A_1B_3}=45,850\)	b

B4 Exemplo: Efeito de Variedades dentro de cada Tratamento de Sementes Teste de Tukey para comparação de médias de Variedades dentro de cada Tratamento de sementes

\[\Delta=q_{(5\%, a, gl \text{Res Composto})}\sqrt{\frac{\text{QM Resíduo Composto}}{r}}=3,88\sqrt{\frac{32,41}{4}}=11,0\]

Variedades dentro de B4 (Agros)}

\(hat{mu}_{A_3B_4} = 56,050\) | \(hat{mu}_{A_2B_4} = 54,300\) | \(hat{mu}_{A_1B_4} = 37,300\) \(hat{mu}_{A_4B_4} = 61,250\) | 5,200 | 6,950 |{23,950} \(hat{mu}_{A_3B_4} = 56,050\) | | 1,750 | {18,750} \(hat{mu}_{A_2B_4} = 54,300\) | | | {17,000}

aula

média	classificação
\(\hat{\mu}_{A_4B_4}=61,250\)	a
\(\hat{\mu}_{A_3B_4}=56,050\)	a
\(\hat{\mu}_{A_2B_4}=54,300\)	a \
\(\hat{\mu}_{A_1B_4}=37,300\)	b

Exemplo: Efeito de Variedades dentro de cada Tratamento de Sementes

aula

-	B1	B2	B3
-	Testemunha	Ceresan M	Panogen
A1 Vicland 1	{36,1} c	{50,6} b	{45,9} b
A2 Vicland 2	{50,9} b	{55,4} ab	{53,1} ab
A3 Clinton	{53,9} ab	{51,4} b	{55,9} ab
A4 Branch	{61,9} a	{63,4} a	{57,7} a

Atividades

Faça o upload da resolução e tire suas aqui