Delineamento quadrado latino
Fundamentos
Características importantes
O número de linhas (\(I\)) é igual ao número de colunas (\(J\)) e igual ao número de tratamento (\(K\)). \(I \;=\; J \;=\; K\)
O número de parcelas no experimento é dado por \(I^2\).
Cada tratamento ocorre uma única vez em cada linha e uma única vez em cada coluna.
O tamanho do experimento cresce rapidamente à medida que aumenta o número de tratamentos.
Os mais comumente encontrados são 5 \(\times\) 5, 6 \(\times\) 6, 7 \(\times\) 7 e 8 \(\times\) 8.
Exemplos
Em ensaios de campo, um terreno (área experimental) pode apresentar declive em dois sentidos, perpendiculares.
Ensaios com animais pode-se ter interesse em testar o efeito de rações distintas, porém o número de animais semelhantes pode ser limitado e ainda ter animais de raças e tamanhos distintos.
LS tree species experiment
(The Forestry Commission)

Croqui: comparação entre DIC, DBC e DQL
#> [1] "T1" "T2" "T3" "T4" "T5" "T6" "T7" "T8" "T9"
#> [1] "A" "B" "C" "D" "E"
#> $parameters
#> $parameters$design
#> [1] "lsd"
#>
#> $parameters$trt
#> [1] "A" "B" "C" "D" "E"
#>
#> $parameters$r
#> [1] 5
#>
#> $parameters$serie
#> [1] 2
#>
#> $parameters$seed
#> [1] -1075533545
#>
#> $parameters$kinds
#> [1] "Super-Duper"
#>
#> $parameters[[7]]
#> [1] TRUE
#>
#>
#> $sketch
#> [,1] [,2] [,3] [,4] [,5]
#> [1,] "B" "A" "C" "E" "D"
#> [2,] "C" "B" "D" "A" "E"
#> [3,] "A" "E" "B" "D" "C"
#> [4,] "D" "C" "E" "B" "A"
#> [5,] "E" "D" "A" "C" "B"
#>
#> $book
#> plots row col Variedades
#> 1 101 1 1 B
#> 2 102 1 2 A
#> 3 103 1 3 C
#> 4 104 1 4 E
#> 5 105 1 5 D
#> 6 201 2 1 C
#> 7 202 2 2 B
#> 8 203 2 3 D
#> 9 204 2 4 A
#> 10 205 2 5 E
#> 11 301 3 1 A
#> 12 302 3 2 E
#> 13 303 3 3 B
#> 14 304 3 4 D
#> 15 305 3 5 C
#> 16 401 4 1 D
#> 17 402 4 2 C
#> 18 403 4 3 E
#> 19 404 4 4 B
#> 20 405 4 5 A
#> 21 501 5 1 E
#> 22 502 5 2 D
#> 23 503 5 3 A
#> 24 504 5 4 C
#> 25 505 5 5 B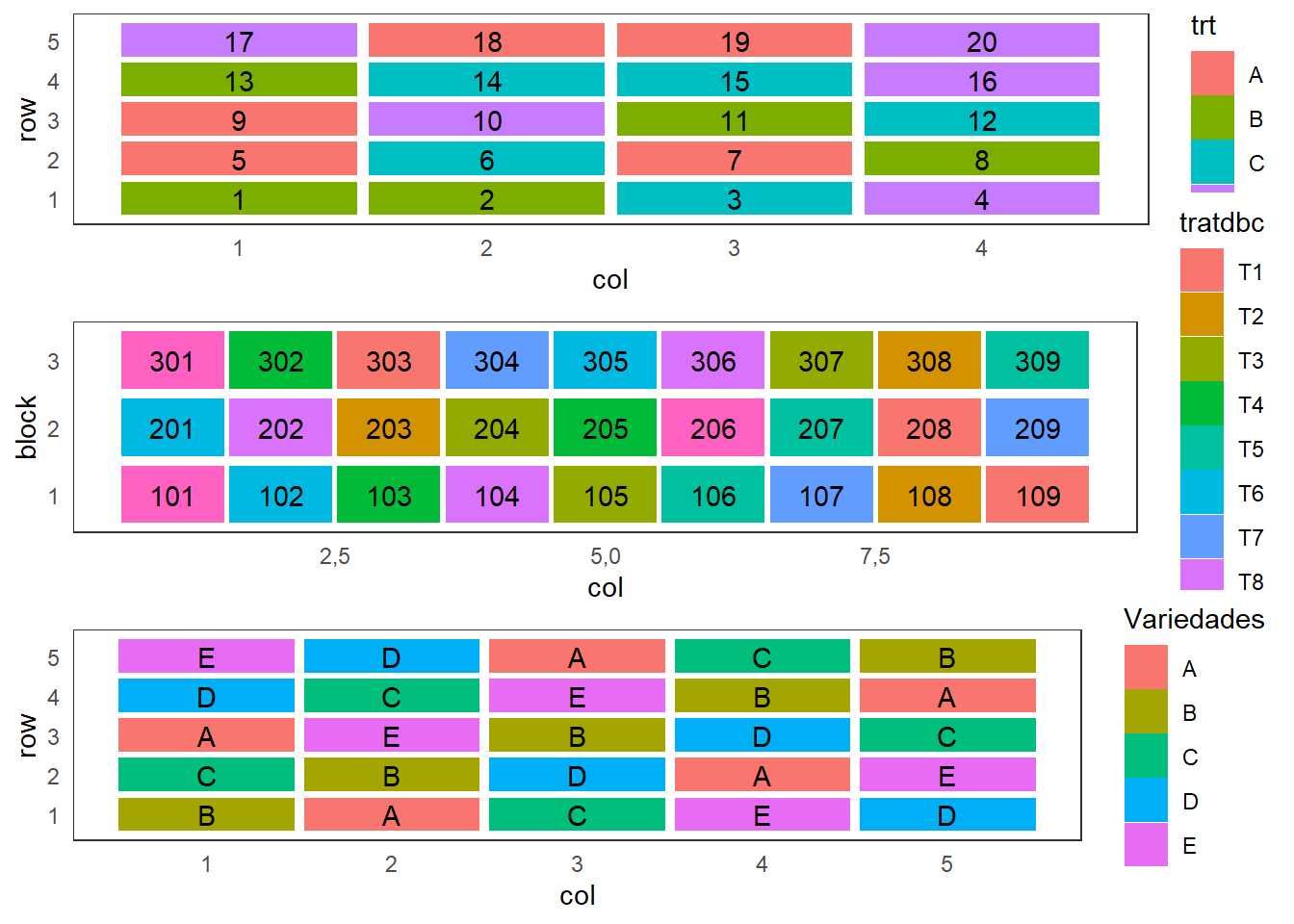
Análise dos dados
Modelo estatístico
\[y_{ij(k)} = \mu + l_i + c_j + \tau_{k(ij)} + e_{ij(k)}, \quad i=1, \ldots, I; j=1, \ldots, I, k=1, \ldots, I,\]
em que:
- \(y_{ij(k)}\) é o valor observação na \(i-\)ésima linha e na \(j\)-ésima coluna (que recebeu o \(k\)-ésimo tratamento);
- \(\mu\) é uma constante comum a todas as observações;
- \(l_i\) é o efeito da \(i-\)ésima linha;
- \(c_j\) é o efeito da \(j\)-ésima coluna;
- \(\tau_{k(ij)}\) é o efeito do \(k\)-ésimo tratamento, e
- \(e_{ijk}\) é o erro experimental, tal que \(e_{ijk} \sim N(0, \sigma^2)\).
DQL: Restrições usuais e estimadores de mínimos quadrados
Restrições
\(\sum_{k=1}^{I} \hat{\tau}_k = 0\)
\(\sum_{i=1}^{I} \hat{l}_i = 0\)
\(\sum_{j=1}^{I} \hat{c}_j = 0\)
Soluções de mínimos quadrados
\(\hat{\mu} = \bar{y}\)
\(\hat{\tau}_k = \bar{y}_k - \bar{y}\)
\(\hat{l}_i = \bar{y}_i - \bar{y}\)
\(\hat{c}_j = \bar{y}_j - \bar{y}\)
Hipóteses de interesse
\(H_0:\) \(\mu_{Trat_1} = \mu_{Trat_2} = \ldots = \mu_{Trat_I}\)
\(H_1:\) \(\text{pelo menos duas médias diferem entre si}\)
Tabela 1. ANOVA
| F.V. | gl | SQ | QM | F |
|---|---|---|---|---|
| Linhas | \(I-1\) | SQL | SQL/glL | QML/QMRes |
| Colunas | \(I-1\) | SQC | SQC/glC | QMC/QMRes |
| Tratamentos | \(I-1\) | SQTra | SQTrat/glTrat | QMTrat/QMRes |
| Resíduo | \((I-1)(I-2)\) | SQRes | QMRes | |
| Total | \(I^2-1\) | SQTotal |
Exemplo
Tabela 2. Produção de 5 variedades de cana-de-açúcar
| Linhas | 1 | 2 | 3 | 4 | 5 | Totais |
|---|---|---|---|---|---|---|
| 1 | 432 (D) | 518 (A) | 458 (B) | 583 (C) | 331 (E) | 2322 |
| 2 | 724 (C) | 478 (E) | 524 (A) | 550 (B) | 400 (D) | 2676 |
| 3 | 489 (E) | 384 (B) | 556 (C) | 297 (D) | 420 (A) | 2146 |
| 4 | 494 (B) | 500 (D) | 313 (E) | 486 (A) | 501 (C) | 2294 |
| 5 | 515 (A) | 660 (C) | 438 (D) | 394 (E) | 318 (B) | 2325 |
| Totais | 2654 | 2540 | 2289 | 2310 | 1970 | 11763 |
\(T_A = 2463 \quad T_B = 2204 \quad T_C = 3024 \quad T_D = 2067 \quad T_E = 2005\)
Soma de quadrados total :
\[SQ_{Total} = \sum_{ij} y_{ij(k)}^2 - \frac{\left(\sum_{ij} y_{ij(k)}\right)^2}{I^2}\\ = 432^2 + 518^2 + \ldots + 318^2 - \frac{11763^2}{25}\\ = 257724,20\]
Soma de quadrados linhas:
\[SQ_{Linhas} = \frac{1}{I}\sum_{i} y_{i.(k)}^2 - \frac{\left(\sum_{ij} y_{ij(k)}\right)^2}{I^2}\\ = \frac{1}{5}\left(2322^2 + 2676^2 + 2146^2 + 2294^2 + 2325^2\right) - \frac{11763^2}{25}\\ = 30480,64\]
Soma de quadrados de colunas
\[SQ_{Colunas} = \frac{1}{I}\sum_{j} y_{.j(k)}^2 - \frac{\left(\sum_{ij} y_{ij(k)}\right)^2}{I^2}\\ = \frac{1}{5}\left(2654^2 + 2540^2 + 2289^2 + 2310^2 + 1970^2\right) - \frac{11763^2}{25}\\ = 55640,64\]
Soma de quadrados de tratamentos
\[SQ_{Tratamentos} = \frac{1}{I}\sum_{k} y_{..k}^2 - \frac{\left(\sum_{ij} y_{ij(k)}\right)^2}{I^2}\\ = \frac{1}{5}\left(2463^2 + 2204^2 + 3024^2 + 2067^2 + 2005^2\right) - \frac{11763^2}{25}\\ = 137488,20\]
Soma de quadrados de resíduos
\[SQ_{\text{Residuo}} = SQ_{\text{Total}} - SQ_{\text{Linhas}} - SQ_{Colunas} - SQ_{Trat} \\ = 257724,20 - 30480,64 - 55640,64 - 137488,20\\ = 34114,72\]
Quadrado médio da linha
\[QM_{Linhas} = \frac{SQ_{Linhas}}{gl_{Linhas}} \\ = \frac{30480,64}{4} \\ = 7620,16\]
Quadrado médio da coluna
\[QM_{Colunas} = \frac{SQ_{Colunas}}{gl_{Colunas}} \\ = \frac{55640,64}{4}\\ = 13910,16\\\]
Quadrado médio do tratamento
\[QM_{Tratamentos} = \frac{SQ_{Tratamentos}}{gl_{Tratamentos}} \\ = \frac{137488,20}{4} \\ = 34372,06\\\]
Quadrado médio do resíduo
\[QM_{Residuo} = \frac{SQ_{Residuo}}{gl_{Residuo}} \\ = \frac{34114,72}{12}\\ = 2842,89\\\]
Tabela 3. Quadro da Anova para o experimento de produção de cana-de-açúcar
| F.V. | gl | SQ | QM | Fcal | Ftab |
|---|---|---|---|---|---|
| Linhas | 4 | 30480,64 | 7620,16 | ||
| Colunas | 4 | 55640,64 | 13910,16 | ||
| Tratamentos | 4 | 137488,20 | 34372,06 | 12,09 | 3,26 |
| Resíduo | 12 | 34114,72 | 2842,89 | ||
| Total | 24 | 257724,20 |
Distribuição F
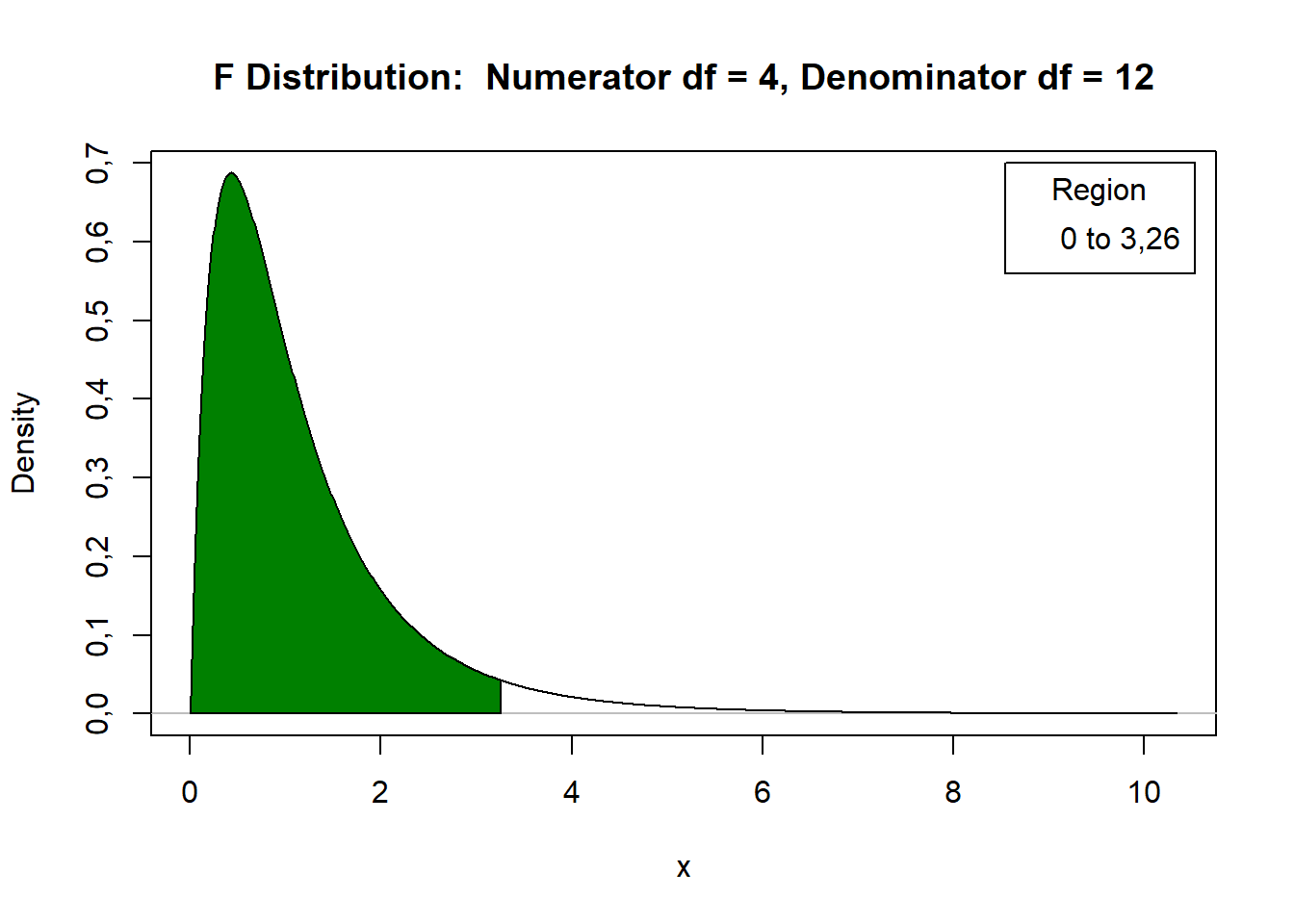
Teste de Tukey
Hipóteses:
- \(H_0\): \(\mu_k = \mu_{k'} \Rightarrow \mu_k - \mu_{k'} = 0\)\
- \(H_1\): \(\mu_k \neq \mu_{k'} \Rightarrow\mu_k - \mu_{k'} \neq 0\)\
\[\Delta = q_{(\alpha, I, glRes)}\sqrt{\frac{\mbox{QM Resíduo}}{J}} = 4,51\sqrt{\frac{2842,89}{5}} = 107,54\]
Tabela 4. Classificação das médias pelo teste de Tukey
| Médias | classificação |
|---|---|
| \(\hat{\mu}_C = 604,8\) | a |
| \(\hat{\mu}_A = 492,6\) | b |
| \(\hat{\mu}_B = 440,8\) | b |
| \(\hat{\mu}_D = 413,4\) | b |
| \(\hat{\mu}_E = 401,0\) | b |
Atividades
Os dados que se seguem referem-se à produção de mandioca, obtidos de um experimento envolvendo quatro sistemas de plantio de manivas de mandioca, instalado no delineamento em quadrado latino 4x4. Esse experimento foi conduzido pela Seção de Raízes e Tubérculos do Instituto Agronômico de Campinas. Os tratamentos envolvidos apresentavam as seguintes características:
- A – Manivas com 0,30 metros, plantadas pelo sistema comum;
- B – Manivas com 0,30 metros, plantadas com 0,15 metros enterradas e inclinadas;
- C – Manivas com 0,30 metros, plantadas com 0,15 metros enterradas, inclinadas e em camaleão;
- D – Manivas com 0,30 metros, plantadas na horizontal na superfície do camaleão.
| Linhas | Colunas | |||
|---|---|---|---|---|
| . | 1 | 2 | 3 | 4 |
| 1 | 122,6 (A) | 98,8 (D) | 122,6 (B) | 102,5 (C) |
| 2 | 126,3 (B) | 110,3 (A) | 110,1 (C) | 53,7 (D) |
| 3 | 83,1 (D) | 106,4 (C) | 100,6 (A) | 93,4 (B) |
| 4 | 96,7 (C) | 107,2 (B) | 75,7 (D) | 80,2 (A) |
Faça o croqui do planejamento de um experimento com as características do experimento em questão.
Com base nos resultados do experimento apresentados na Tabela 2 e considerando o nível de significância 5%:
- Ajuste o modelo e verifique as pressuposições do modelo;
- Faça a análise de variância e conclua;
- Compare as médias dos tratamentos usando o teste Tukey e tire conclusões;
- Elabore um grupo de contrastes ortogonais de interesse prático e teste-os.
- A análise apresentada a seguir é referente aos dados de um experimento instalado para avaliar o efeito do tempo de castração (7, 21, 56 dias ou não castração) no ganho de peso de suínos. Com base no quadro da ANOVA apresentado a segui, pede-se:
| F.V. | gl | SQ | QM | Fcal | Ftab |
|---|---|---|---|---|---|
| Linhas | 436,555 | ||||
| Colunas | 148,945 | ||||
| Tratamentos | 913,575 | 4,75 | |||
| Resíduo | 412,995 | ||||
| Total | 1912,070 |
- complete o quadro da anova
Resolução
F.V. gl SQ QM Fcal Ftab Linhas 3 436,555 Colunas 3 148,945 Tratamentos 3 913,575 304,52 4,42 4,75 Resíduo 6 412,995 68,33 Total 15 1912,070
Ao nível de 5% de significância, há evidências para rejeitarmos \(H_0\). Logo, não podemos afirmar que todas as médias de ganho de peso para os diferentes tratamentos são iguais.
Faça o upload da resulução e tire suas aqui