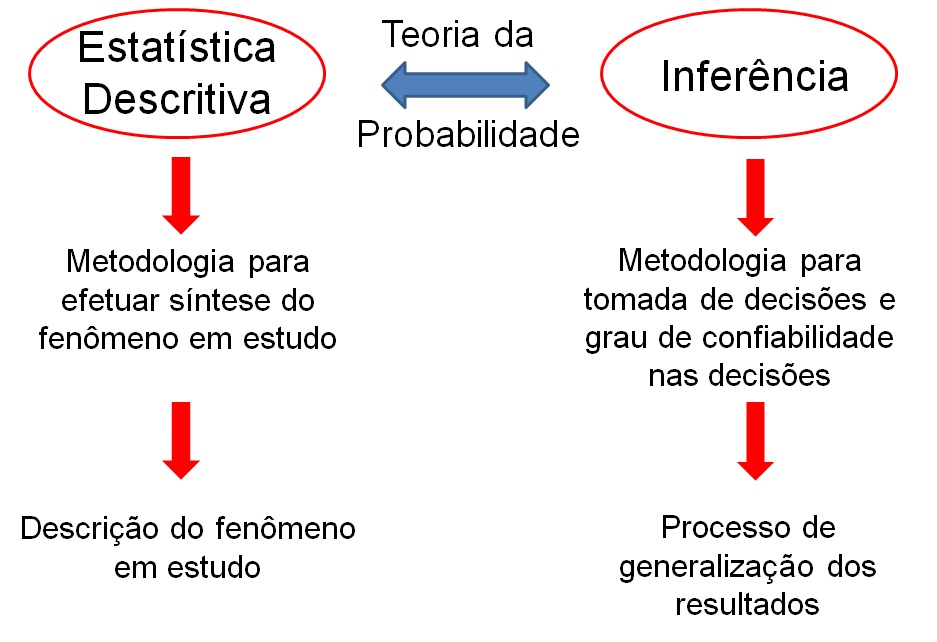
Estatística nas ciências agrárias

    Segundo o dicionário Michaelis a estatística é o ramo da matemática responsável que tem por objetivo a coleção, análise e interpretação de dados numéricos a respeito de fenômenos coletivos ou de massa. Realizar a representação numérica e comparativa, em tabelas ou gráficos, dos resultados da análise desses fenômenos.
Fluxograma
Fluxograma

  • Levantamento: Observa-se o fenômeno como ele é na natureza

  • Experimento: Nesse caso, as observações são geradas e feitas, comumente, sob condições controladas pelo pesquisador, e os fatos, eventos ou fenômenos são forçados a sofrer variações sistemáticas mediante aplicação de tratamentos. Pretende-se determinar relações de causa e efeito.

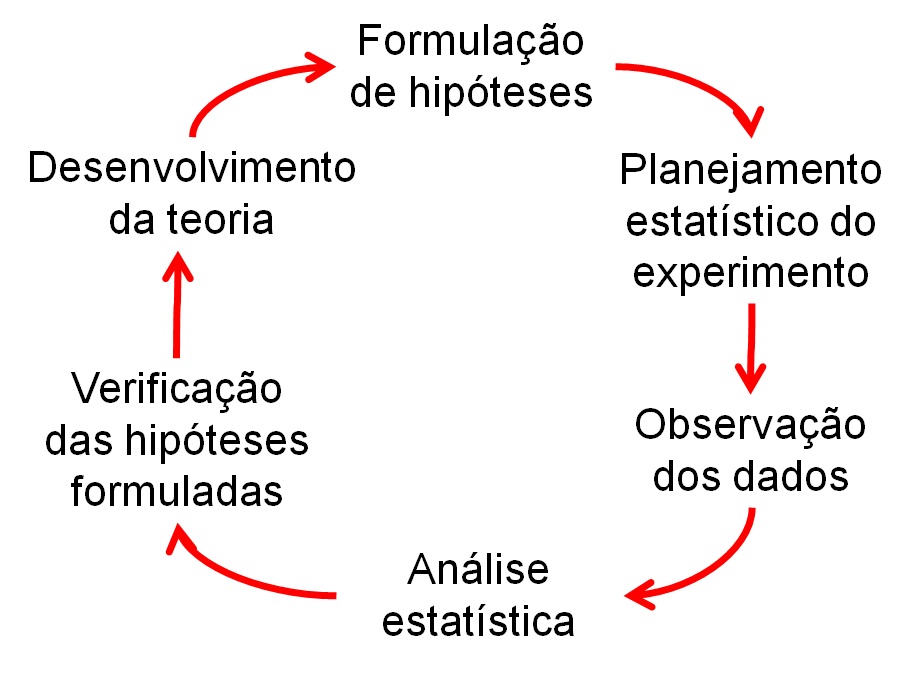
Método científico

métodocientífico
métodocientífico
campos
campos
pop
pop
bordadura
bordadura

Conceitos iniciais

Parâmetro: são quantidades da população, em geral desconhecidas, sobreas quais tem-se interesse.

Estimativa: são valores numéricos associados aos parâmetros, obtidos a partir de uma amostra.

Estimadores pontuais

\[\mbox{Média: } \hat{\mu} = \bar{X} = \frac{\sum_{i=1}^n X_i}{n}\]

\[\mbox{Variância: } \hat{\sigma}^2 = S^2 = \frac{\sum_{i=1}^n(X_i-\bar{X})^2}{n-1}\]

\[\mbox{Desvio-padrão: } \hat{\sigma} = S = \sqrt{\frac{\sum_{i=1}^n(X_i-\bar{X})^2}{n-1}}\]

\[\displaystyle{\mbox{Coeficiente de variação: } 100 \times \frac{\sqrt{\hat{\sigma}^2}}{\hat{\mu}}\%.}\]

Mediana, Quartis e Percentis

  • Mediana: corresponde ao valor central de um conjunto de valores ordenados.

  • Quartis: valores que dividem uma amostra de dados ordenados em quatro partes iguais.

  • Percentis de ordem \(100p\): valores que dividem a amostra ordenada em 100 partes aproximadamente iguais.

Gráfico de Caixas

O gráfico de caixas é uma importante ferramenta para o estudo da simetria das distribuições e detecção de observações atípicas.

Construção de um gráfico de caixas

  • Calcular o primeiro quartil (\(Q_1\)), a mediana (Md) e o terceiro quartil (\(Q_3\));
  • Calcular a distância interquartílica: AIQ = \(Q_3 - Q_1\);
  • Verificar a existência de observações atípicas, ou seja, valores menores do que \(Q_1-1,5\mbox{AIQ}\) ou maiores do que \(Q_3+1,5\mbox{AIQ}\), representados individualmente no gráfico de caixas por \(\ast\);
  • Calcular os limites inferior e superior dos dados sem considerar as observações atípicas;
  • Construir o gráfico seguindo o esquema a seguir:

Gráfico 1: Exemplo Boxplot

boxplot(c(11.5, 18.7,   15,
       17.6,    12.4,   21,
       14.4,    15.2,   16.9,   14.5,
       16.2,    14.1,   15.7,   16,
       15.7,    13.1,   15.2,   18,
       15.1,    19.6,
       18.1,    14.7,   16.4,   13.8,
       18.8,    15.5,   17.6,   16.8,
       15.2,    13.7))

Estimadores intervalares

Intervalo de confiança

    Seja (\(X_1, X_2, \ldots, X_n\)) uma amostra aleatória de tamanho \(n\) de uma população e \(\theta\) o parâmetro de interesse. Sejam \(\hat{\theta}_1\) e \(\hat{\theta}_2\) estatísticas tais que:

\[P(\hat{\theta}_1 < \theta < \hat{\theta}_2) = 1-\alpha.\]

     Então o intervalo \((\hat{\theta}_1; \hat{\theta}_2)\) é chamado intervalo de {} para o parâmetro \(\theta\).Usualmente, toma-se \(1-\alpha\) = 0,95 ou 0,99.
     Interpretação: De todos os possíveis intervalos que possam ser construídos, espera-se que \(100(1-\alpha)\%\) deles contenham o valor verdadeiro do parâmetro \(\theta\).

Intervalo de confiança para a média

\[{IC(\mu)_{1-\alpha} = \Bigg(\bar{X}-t_T\sqrt{\frac{\hat{\sigma}^2}{n}}; \bar{X}+t_T\sqrt{\frac{\hat{\sigma}^2}{n}} \Bigg)}\]

para \(n \geq 30\)

\[{IC(\mu)_{1-\alpha} = \Bigg(\bar{X}-z_T\sqrt{\frac{\hat{\sigma}^2}{n}}; \bar{X}+z_T\sqrt{\frac{\hat{\sigma}^2}{n}} \Bigg)}\]

Classificação de variáveis:

     Natureza dos dados Observação ou dados estatísticos: valor específico da variável, podendo ser qualitativo ou quantitativo.

  • Variável qualitativa: apresenta como realização uma qualidade ou atributo do indivíduo pesquisado.

  • Variável qualitativa nominal: não apresenta ordenação nas possíveis realizações.

  • Variável qualitativa ordinal: existe uma ordenação natural nas possíveis realizações.

  • Variável quantitativa: as possíveis realizações são mensuráveis.

  • Variável quantitativa discreta: os possíveis valores formam um conjunto finito ou infinito e enumerável (contagens). Irmãos.

Variável quantitativa contínua: os possíveis valores formam um intervalo de números reais (mensurações).

Atividade

  1. Os pesos ao nascer de 12 bezerros machos da raça holandelesa são os seguintes, em kg:
A B C D E F G H I J K L
47 41 34 45 45 46 25 48 37 47 40 40
  1. Apresentar uma análise descritiva do conjunto de dados. Calcule:
  • Média;
  • Moda;
  • Mediana;
  • Variância;
  • Desvio-padrão;
  • Construa um gráfico boxplot;

Faça o upload da resolução e tire suas aqui