Delineamento inteiramente casualizado
Fundamentos
Exemplo: Vinhedo

Figura 1: Dois experimentos em DIC com quatro repetições de um tratamento (linhas amarelas) e de um controle (linhas azuis), sendo um em um vinhedo pequeno (A) e outro em um vinhedo médio (C). Fonte: Hemant Gohil.
Note que os exemplos consideram uma linha de bordadura entre as linhas.
Em alguns casos o mesmo tratamento ocupa parcelas vizinhas .
Os croquis para os ensaios mostrados em A e C são exibidos em B e D, respectivamente.
Obtendo um croqui para um DIC
- Enumerar as parcelas 1, 2, . . . , \(n\)
- Criar o delineamento sistemático, ou seja, alocar o tratamento 1 às parcelas 1, 2, . . . , \(n_1\) alocar o tratamento 2 às parcelas \(n_1\) + 1, \(n_1\) + 2, . . . , \(n_1\) + \(n_2\) e assim até as repetições do tratamento \(I\).
- Escolha uma permutação de 1, 2, . . . , \(n\) e aplique ao delineamento.
Exemplo
| Ordem Padrão | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Variedade | A | A | A | B | B | B | B | C | C | C |
Uma permutação:
| Parcelas | 7 | 1 | 8 | 10 | 3 | 2 | 4 | 6 | 9 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|
| Ordem Padrão | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
E o plano de casualização é dado por:
| Parcelas | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Variedade | B | A | C | C | A | A | B | B | C | A |
Análise dos dados
Modelo estatistico
\[\begin{equation} y_{ij} = \mu + \tau_i + e_{ij} = \mu_i + e_{ij} \text{(2)} \end{equation}\]
em que:
\(y_{ij}\) é o valor observado na j-ésima repetição do iésimo tratamento, com:
\(i = 1, ... , I\) e
\(j = 1, ... , n_i\)
\(\mu\) é uma constante inerente a todas as observações, geralmente a média geral,
\(\tau_i\) é o efeito do iésimo tratamento,
\(e_{ij}\) é o erro experimental, tal que \(e_{ij} \overset{iid}{\sim} N(0,\sigma^2)\).
\[H_0 : \tau_{1} = \tau_{2} = ... = \tau_{I} = 0\]
\[H_1 = H_a : \tau_{i} \neq 0\]
\[y_{ij} = \alpha_i + e_{ij} \text{(3)}\]
\[H_0 : \alpha_1 = \alpha_2 = ... = \alpha_I = \mu\]
\[H_1 = Ha : \text{pelo um contraste de médias difere de zero}\].
Desse modo, a esperança da variável aleatória \(Y_{ij}\) será
\[E(Y_{ij}) = E(\mu + \tau_i + E_{ij} ) = \mu + \tau_i + 0 = \mu + \tau_i \text(4)\]
Análise de variância
Tabela 1: Demonstração sobre fontes de variação e graus de liberdade
| Fontes de Variação | Graus de liberdade |
|---|---|
| Total | \(n\text{-}1\) |
| Tratamentos | \(I\text{-}1\) |
| Resíduo | \(n\text{-}I\) |
\[\text{Variância} = \sum _{ij} \frac{(yij−\bar{y})^2}{(n−1)} (\text{expressão 1})\]
\[\text{variância} = \displaystyle{\frac{\text{SQ}}{\text{gl}}}(\text{expressão 2})\]
\[\text{F} = \displaystyle{\frac{\text{QM}_{\text{Trat}}}{\text{QM}_{\text{Resíduo}}}}\]
Retomando as hipóteses
\(H_0 : \mu_1 = \mu_2 = ... = \mu_I = 0\)
\(H_1 = Ha\): pelo um contraste de médias difere de zero.Denotamos por Soma de Quadrados do Total (SQ Total) o numerador da expressão 2. Observe que a decomposição mencionada anteriormente será:
\[\displaystyle{\sum_{i=1}^I\sum_{j=1}^Jy_{ij}^2\text-\frac{\left(\sum_{i=1}^I\sum_{j=1}^Jy_{ij}\right)^2}{I\times J}}(\text{expressão 3})\]
As expressões apresentadas em 4 e 5, podem ser reescritas conforme segue.
\[\displaystyle{\frac{1}{J}\sum_{i=1}^I T_i^2 \text- \frac{\left(\sum_{i=1}^I\sum_{j=1}^Jy_{ij}\right)^2}{I\times J}}(\text{expressão 4})\]
SQ Resíduo = SQ Total - SQ Tratamentos.
Os quadrados médios, denotados usualmente por QM, são definidos pelo quociente entre a soma de quadrados e o respectivo número de graus de liberdade relacionados a uma fonte de varição, isto é:
\[\text{QM}_{\text{Trat}} = \displaystyle{\frac{\text{SQ}_\text{Trat}}{\text{gl}_\text{Trat}}}\]
Coeficiente de variação
O CV é adimensional, pode-se comparar a dispersão de variáveis com diferentes unidades de medida.
\[\displaystyle{\text{CV}_{\%} = 100\frac{\hat{\sigma}}{\hat{\mu}} = 100\frac{\sqrt{\text{QM}_{\text{Res}}}}{\bar{y}}}\]
CV \(<\) 10% : baixo
10% \(<\) CV \(>\) 20% :médio
20% \(<\) CV \(>\) 30% :alto
CV \(>\) 30% : muito alto
Exemplo
Tabela 2: produtividade de milho (kg/100m\(^2\)) de quatro diferentes variedades
| (Variedades) | 1 | 2 | 3 | 4 | 5 | total | média |
|---|---|---|---|---|---|---|---|
| A | 25 | 26 | 20 | 23 | 21 | 115 | 23,00 |
| B | 31 | 25 | 28 | 27 | 24 | 135 | 27,00 |
| C | 22 | 26 | 28 | 25 | 29 | 130 | 26,00 |
| D | 33 | 29 | 31 | 34 | 28 | 155 | 31,00 |
Tabela 3: nomenclatura de dados
| (Variedades) | 1 | 2 | 3 | 4 | 5 | total |
|---|---|---|---|---|---|---|
| V1 | y11 | y12 | y13 | y14 | y15 | y1· = T1 |
| V2 | y21 | y22 | y23 | y24 | y25 | y2· = T2 |
| V3 | y31 | y32 | y33 | y34 | y35 | y3· = T3 |
| V4 | y41 | y42 | y43 | y44 | y45 | y4· = T4 |
Análise descritiva:
Tabela 4: Análise descritivas dos dados
| Análise | A | B | C | D |
|---|---|---|---|---|
| Soma | 115,00 | 135,00 | 130,00 | 155,00 |
| Média | 23,00 | 27,00 | 26,00 | 31,00 |
| Variância | 6,50 | 7,50 | 7,50 | 6,50 |
| Desvio-padrão | 2,55 | 2,74 | 2,74 | 2,55 |
Soma de Quadrados total
\[\text{SQ}_{\text{Total}} = \displaystyle{\sum_{i=1}^4\sum_{j=1}^5y_{ij}^2 \text{-} \frac{\left(\sum_{i=1}^4\sum_{j=1}^5y_{ij}\right)^2}{4\times5}}\]
\[ = \displaystyle{25^2 + 26^2 + \ldots + 28^2 \text{-} \frac{535^2}{20}} = 275,75\]
Soma de Quadrados de tratamentos
\[\text{SQ}_{\text{Trat}} = \displaystyle{\frac{1}{5}\sum_{i=1}^4 T_i^2 \text{-} \frac{\left(\sum_{i=1}^4\sum_{j=1}^5y_{ij}\right)^2}{4\times5}}\]
\[= \displaystyle{\frac{1}{5}\left(115^2 + 135^2 + 130^2 + 155^2\right) - \frac{535^2}{20}}= 163,75\]
Soma de Quadrados do Resíduo
\[\text{SQ}_\text{Resíduo} = \text{SQ}_{\text{Total}} \text{-} \text{SQ}_{\text{Trat}}\] \[= 275,75 - 163,75 = 112,00\]
Quadrado médio tratamentos
\[\text{QM}_{\text{Trat}} = \displaystyle{\frac{\text{SQ}_{\text{Trat}}}{\text{gl}_{\text{Trat}}}} = \displaystyle{\frac{163,75}{3}} = 54,5833\]
Quadrado médio do resíduo
\[\text{QM}_{\text{Resíduo}} = \displaystyle{\frac{\text{SQ}_{\text{Resíduo}}}{\text{gl}_{\text{Resíduo}}}}=\displaystyle{\frac{112,00}{16}}= 7,0000\]
F calculado
\[\text{F} = \displaystyle{\frac{\text{QM}_{\text{Trat}}}{\text{QM}_{\text{Resíduo}}}}=\displaystyle{\frac{54,5833}{7,0000}}= 7,80\]
Tabela 5: ANOVA
| Fontes | Graus de liberdade | Soma de Quadrados | Quadrado Médio | Fcal | Ftab |
|---|---|---|---|---|---|
| Tratamentos | 3 | 163,75 | 54,5833 | 7,80 | |
| resıduo | 16 | 112,00 | 7,0000 | ||
| Total | 19 | 275,75 |
F tabelado:
# Defina o nível de significância desejado (por exemplo, 0.05 para um nível de 5%)
nivel_de_significancia <- 0.05
# Defina os graus de liberdade do numerador (df1) e do denominador (df2)
df1 <- 3 # Graus de liberdade do numerador
df2 <- 16 # Graus de liberdade do denominador
# Encontre o valor crítico da distribuição F para o nível de significância especificado
valor_critico <- qf(1 - nivel_de_significancia, df1, df2)
# Imprima o valor crítico
cat("Valor crítico da distribuição F:", valor_critico, "\n")
#> Valor crítico da distribuição F: 3,238872Distribuição F
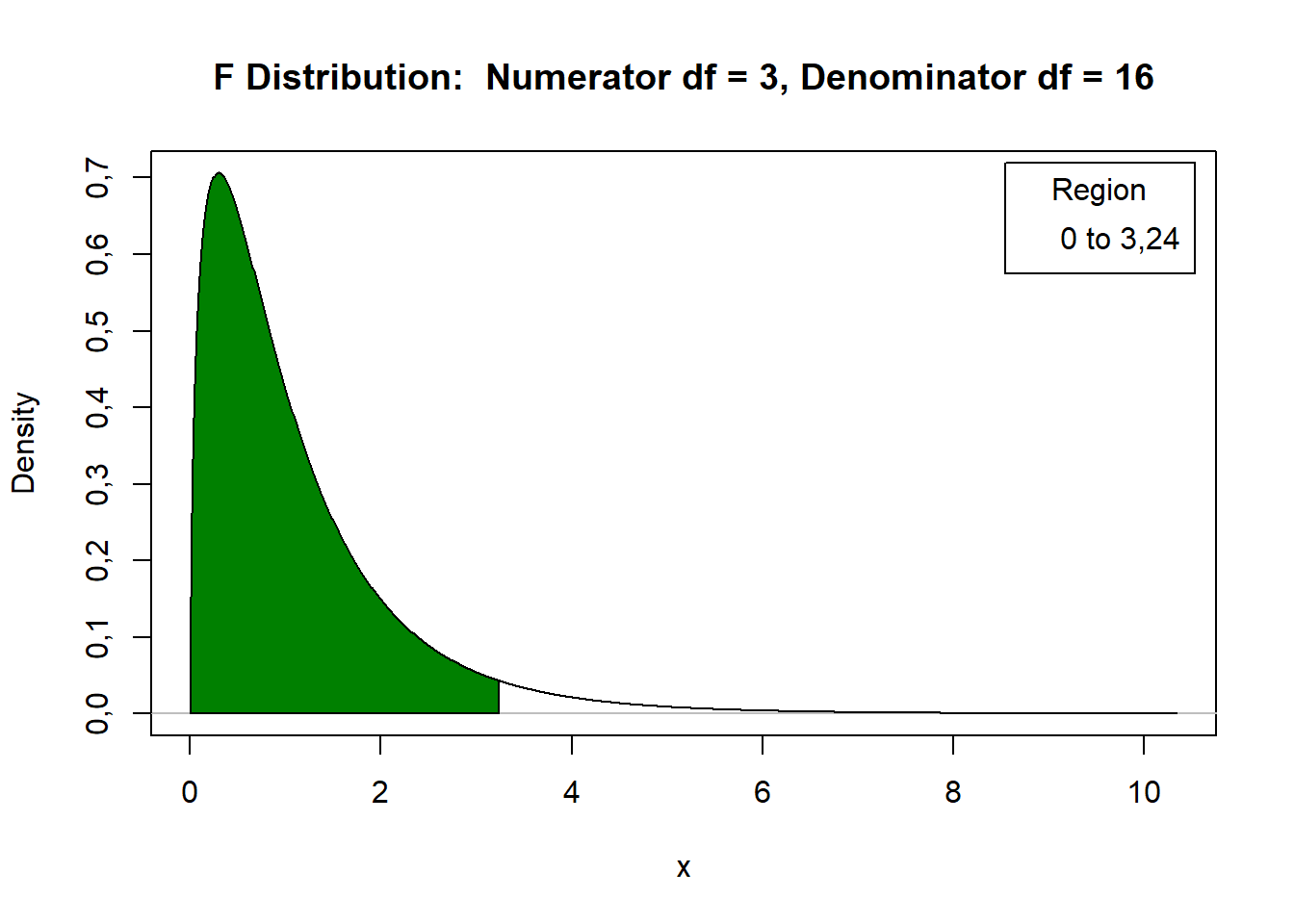
Como \(\text{F} = 7. 80 > 3. 24 = \text{FTab}\) (\(\alpha = 0. 05, 3, 16\)), há evidências para rejeitarmos \(H_0\) ao nível de 5% de significância. Desse modo, não podemos afirmar que todas as médias são iguais.
Atividade
- Responda verdadeiro ou falso:
Para estudar o efeito de 3 manejos na cultura da cana-de açúcar, um pesquisador fez um experimento coletando os teores de açúcar de 5 colmos e analisou a média dos mesmos. O experimento foi instalado seguindo as curvas de nível do local no delineamento inteiramente casualizado.
O quadrado médio do resíduo representa a variância do experimento.
- Em um experimento de competição de dez cultivares de arroz para avaliar a produtividade, instalado em um delineamento inteiramente casualizado, os resultados (parciais) para a ANOVA foram os seguintes:
- Complete o quadro da ANOVA
| Fonte | GL | SQ | QM | F Cal | F Tab |
|---|---|---|---|---|---|
| cultivar | 17564523 | 9.31 | 2.39 | ||
| Resíduo | |||||
| Total | 29 |
Variável resposta:
Tratamento:
Parcelas:
Faça o upload da resolução e tire suas aqui